
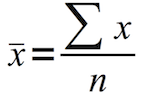
Even in company C, which has the flattest salary distribution, 14 out of 17 employees (82%) receive less than the average. The difference in individual salaries is quite obvious, yet the mean is the same for all three companies: $57,705.88 yearly. Here is the same data on the same coordinate system: Also note that the Y-axis is not on the same scale for all three graphs. Take for example these 3 sets of data, each for 17 employees from three different companies: A, B, and C:Īll of the above have the same arithmetic average, despite the different range and distribution. When the mean of a set does not tell us much However, nowadays we have very powerful and very easy ways to show the whole set of data, the whole distribution, so presenting only the arithmetic mean may be a bad practice. Averages were widely used before the invention of computers when plotting or otherwise visualizing even moderately large sets of data was a huge task, and few people could understand the graphs.
#THE ARTMATIC MEAN HOW TO#
How to not be mislead by averagesĪs with any single number that is used to represent a set of data, a mean is bound to be an incomplete, and in a sense inaccurate representation. These are all reasons to make use of our arithmetic average calculator.

a survey), the sample mean is a statistically unbiased estimator for the population mean. For samples drawn from a population (e.g. Another great property is that it minimizes the sum of squared deviations (has the lowest root mean squared error - sum of (x i - x) 2) so it serves as the best single predictor for the set. The properties that make the arithmetic mean useful are that the numbers to the left of the mean are balanced by the numbers to the right of the mean, in other words - the residuals, or the derivations from the estimate, sum up to zero. Useful properties of the arithmetic average For example, if the numbers are 2, 4, and 6 their arithmetic average can be found by summing 2, 4, and 6, and then dividing them by their count (3), resulting in (2 + 4 + 6) / 3 = 12 / 3 = 4. To find the mean simply replace the values at hand in the formula and solve the simple equation. N is, of course, the number of elements in the set of data. The symbolic representation of the formula is: This mean calculator does not support weighted averages as they require a more advanced set of inputs. In some cases a "mean" or an "average" may refer to a weighted average, in which different weights are assigned to different points of the data set based on some characteristic of theirs. In some cases, this is a desired property, while in others it makes the simple mean unsuitable for purpose. For example, adding the number 99 to the previous set of numbers will increase the mean from 4.5 to 18, which is significantly larger than all but one of the values in the set. The mean is not a robust statistic, meaning that it is greatly influenced by outliers / extreme values. As you may note, the number 4.5 is not a part of the original set of numbers, and that is quite common.
x n.įor example, the arithmetic mean of the set 1, 2, 3, 4, 7, 10 is 1 + 2 + 3 + 4 + 7 + 10 / 6 = 4.5 (verified using this arithmetic mean calculator). In statistics the mean is usually denoted with a bar, say x (read "x bar"), meaning the mean of values x 1, x 2. The term "average" is sometimes used to describe other statistics, such as the median or the mode, while the term "mean" can refer to other means, such as the geometric mean or the harmonic mean, which is why the term "arithmetic mean" is preferred for clarity. It is calculated by summing up all numbers in a data set, then dividing by the number of data items and is the most readily understood measure of central tendency. The mean, often called just "average" or "mean", is a descriptive statistic used as a summary measure of an attribute of a sample (dataset). The arithmetic mean is one of the most commonly used statistics.



 0 kommentar(er)
0 kommentar(er)
